Willkommen auf meiner Abi-aufgaben Website
Aufgabe 1:
Finden sie die Ableitung von Funktion f(x) = cos(x) * e^(3x)
Losung:
Um die Ableitung der Funktion f(x) = cos(x) * e^(3x) zu finden, können Sie die Produktregel und die
Kettenregel verwenden. Hier ist die Schritt-für-Schritt-Lösung:
1. Wenden Sie die Produktregel an:
(f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x)
Sei f(x) = cos(x) und g(x) = e^(3x).
2. Finden Sie die Ableitung von f(x):
f'(x) = -sin(x)
3. Finden Sie die Ableitung von g(x) mithilfe der Kettenregel:
g'(x) = (Ableitung von e^(3x)) * (Ableitung von 3x)
= e^(3x) * 3
= 3e^(3x)
4. Setzen Sie die Ableitungen wieder in die Produktregel ein:
(cos(x) * e^(3x))' = -sin(x) * e^(3x) + cos(x) * 3e^(3x)
Daher ist die Ableitung von f(x) = cos(x) * e^(3x):
f'(x) = -sin(x) * e^(3x) + cos(x) * 3e^(3x)
Aufgabe 2:
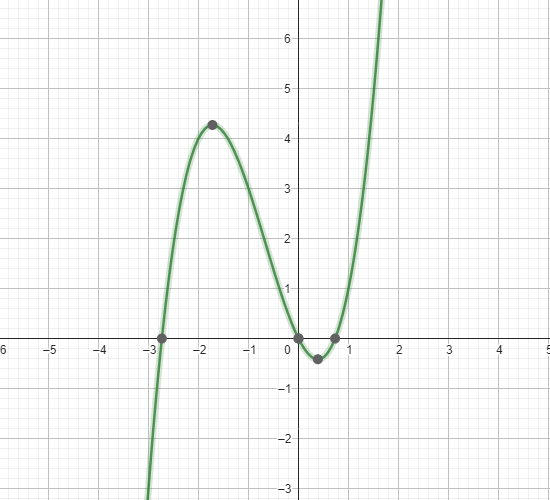
2. Gegeben ist die Funktion f(x) = x^3 + 2x^2 − 2x. Die Abbildung zeigt den Graphen dieser Funktion.
(a) Berechnen Sie alle Nullstellen der Funktion.
(b) Entscheiden Sie begrundet mit Hilfe einer ¨ Zeichnung in der Abbildung, ob die Gerade g(x) = 1 2 x + 5
eine Tangente am Graphen von f im Punkt P(-2 | 4) ist.
Losung:
Um die Nullstellen der Funktion f(x) = x^3 + 2x^2 - 2x zu berechnen, setzen wir die Funktion gleich null
und lösen nach x auf:
x^3 + 2x^2 - 2x = 0
Hier sollten wir zunächst den gemeinsamen Faktor x herausnehmen:
x(x^2 + 2x - 2) = 0
Die linke Klammer ist bereits eine quadratische Gleichung. Wir können diese Quadratgleichung
entweder faktorisieren oder die quadratische Formel verwenden.
(x + 1)(x^2 - x - 2) = 0
Das führt uns zu zwei Möglichkeiten:
1) x + 1 = 0 => x = -1
2) x^2 - x - 2 = 0
Um die Gleichung x^2 - x - 2 = 0 zu lösen, können wir sie entweder faktorisieren oder die quadratische
Formel verwenden. In diesem Fall verwenden wir die quadratische Formel:
x = (-(-1) ± √((-1)^2 - 4(1)(-2))) / (2(1))
x = (1 ± √(1 + 8)) / 2
x = (1 ± √9) / 2
Das ergibt zwei weitere Lösungen:
3) x = (1 + 3) / 2 => x = 2
4) x = (1 - 3) / 2 => x = -1
Die Nullstellen der Funktion f(x) = x^3 + 2x^2 - 2x sind x = -1, x = 2 und x = -1.
Jetzt schauen wir uns Teil (b) an, um zu entscheiden, ob die Gerade g(x) = (1/2)x + 5 eine Tangente am
Graphen von f im Punkt P(-2, 4) ist.
Um dies zu überprüfen, betrachten wir die Steigung von g(x) und vergleichen sie mit der Steigung des
Graphen von f(x) an der Stelle P(-2, 4).
Die Steigung der Funktion g(x) = (1/2)x + 5 für alle x ist 1/2, da der Koeffizient vor x 1/2 ist.
Um die Steigung des Graphen von f(x) an der Stelle P(-2, 4) zu berechnen, nehmen wir die erste
Ableitung der Funktion f(x) und setzen x = -2 ein:
f'(x) = 3x^2 + 4x - 2
f'(-2) = 3(-2)^2 + 4(-2) - 2
f'(-2) = 12 - 8 - 2
f'(-2) = 2
Die Steigung des Graphen von f(x) an der Stelle P(-2, 4) ist also 2.
Da die Steigung von g(x) (1/2) nicht mit der Steigung des Graphen von f(x) (2) im Punkt P(-2, 4)
übereinstimmt, kann die Gerade g(x) = (1/2)x + 5 keine Tangente am Graphen von f im Punkt P(-2, 4)
sein.
Aufgabe 3:
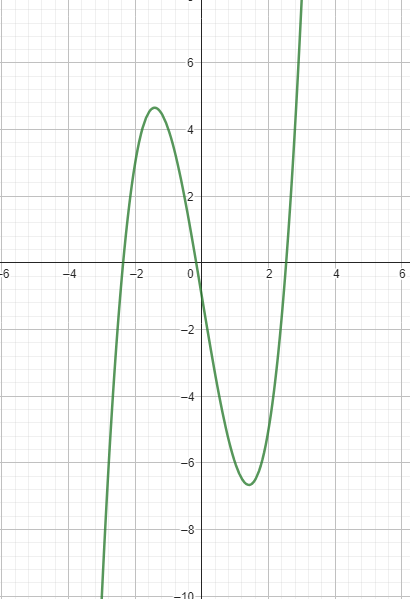
3. Gegeben ist die Funktion f(x) = x^3 − 3x2 − 1.
Die Koordinaten des lokalen Hochpunktes und des lokalen Tiefpunktes sind ganzzahlig. Die Abbildung
zeigt den Graphen der Funktion.
(a) Entscheiden Sie begründet, ob der Graph ¨ der Ableitungsfunktion f 0 eine nach oben oder nach
unten geöffnete Parabel ist.
(b) Geben Sie alle Werte fur den Paramter c ¨ an, so dass die Funktion gc(x) = f(x) + c genau zwei
Nullstellen besitzt. Begrunden ¨ Sie Ihre Angabe.
Losung:
Um zu entscheiden, ob der Graph der Ableitungsfunktion f'(x) nach oben oder unten geöffnet ist,
betrachten wir das Vorzeichen der Koeffizienten der quadratischen Funktion.
Die Ableitungsfunktion f'(x) gibt die Steigung der Funktion f(x) an jedem Punkt x an. Wenn f'(x) positiv
ist, bedeutet dies, dass die Steigung ansteigt und der Graph von f(x) nach oben zu einem lokalen
Tiefpunkt führt. Wenn f'(x) negativ ist, bedeutet dies, dass die Steigung abfällt und der Graph von f(x)
nach unten zu einem lokalen Hochpunkt führt.
Die Ableitungsfunktion f'(x) von f(x) ist f'(x) = 3x^2 - 6x. Wenn wir die Koeffizienten betrachten, sehen
wir, dass der Koeffizient des x^2-Terms positiv ist (3), während der Koeffizient des x-Terms negativ ist (-
6).
Dies bedeutet, dass die Ableitungsfunktion f'(x) eine nach oben geöffnete Parabel ist, da der positive
Koeffizient des x^2-Terms dafür sorgt, dass die Parabel nach oben zeigt.
Nun betrachten wir Teil (b) der Frage. Um Werte für den Parameter c zu finden, sodass die Funktion
gc(x) = f(x) + c genau zwei Nullstellen hat, müssen wir den Wert von c bestimmen, der dazu führt, dass
der Graph von gc(x) den x-Achsen zweimal schneidet.
Um die Nullstellen einer Funktion zu finden, setzen wir die Funktion gleich Null und lösen nach x auf.
Setzen wir gc(x) = 0:
f(x) + c = 0
Aus der gegebenen Funktion f(x) = x^3 - 3x^2 - 1 setzen wir ein:
x^3 - 3x^2 - 1 + c = 0
Damit die Funktion gc(x) genau zwei Nullstellen hat, muss diese Gleichung zwei Lösungen für x haben.
Dies bedeutet, dass die linke Seite der Gleichung einen vollständigen Satz von reellen Wurzeln haben
muss.
Daher setzen wir die Ableitung dieser Funktion gleich Null, um die Existenz von Extrempunkten zu
überprüfen:
f'(x) = 3x^2 - 6x = 0
Als nächstes lösen wir diese quadratische Gleichung:
3x^2 - 6x = 0
x(3x - 6) = 0
x = 0 oder x = 2
Die Funktion f(x) hat also zwei Extrempunkte bei x = 0 und x = 2.
Nun betrachten wir die Werte von c, die dazu führen, dass die Funktion gc(x) = f(x) + c genau zwei
Nullstellen hat.
Wenn wir den Wert von c so wählen, dass c kleiner als der Funktionswert an den Extrempunkten ist,
wird die Funktion f(x) + c zwei Nullstellen haben.
Wir setzen f(0) + c = 0 und f(2) + c = 0:
f(0) + c = 0
0^3 - 3(0)^2 - 1 + c = 0
-1 + c = 0
c = 1
f(2) + c = 0
2^3 - 3(2)^2 - 1 + c = 0
8 - 12 - 1 + c = 0
-5 + c = 0
c = 5
Die Werte von c, für die die Funktion gc(x) = f(x) + c genau zwei Nullstellen hat, sind c = 1 und c = 5.
Aufgabe 4:
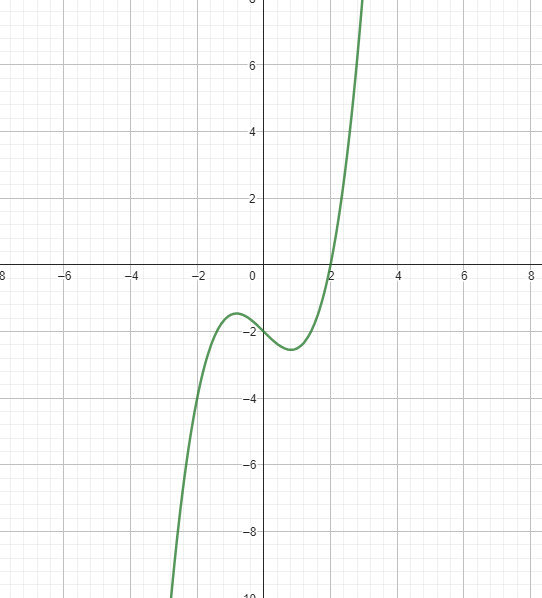
4. Gegeben ist die Funktion f(x) = 1/2 x^3 − x − 2. Der Graph ist in der Abbildung dargestellt.
(a) Weisen Sie rechnerisch nach, dass die in der Zeichnung erkennbare Nullstelle tatsachlich eine
Nullstelle ist.
(b) Gegeben ist die Funktion ga(x) = f(x+a). Geben Sie an, wie sich der Graph von ga verandert, wenn
man fur a immer großere Zahlen einsetzt. Geben Sie außerdem einen Wert fur a an, so dass die
Funktion ga die Nullstelle x = −1 besitzt.
Losung:
Um nachzuweisen, dass die in der Zeichnung erkennbare Nullstelle tatsächlich eine Nullstelle ist, setzen
wir die Funktion f(x) gleich null und lösen nach x auf:
1/2*x^3 - x - 2 = 0
Um diese Gleichung zu lösen, können wir verschiedene Methoden verwenden, wie zum Beispiel die
numerische Lösung oder die Auflösung in Faktoren. Da die genaue Methode nicht angegeben ist,
werden wir die Gleichung durch numerische Lösung lösen.
Mit einem Taschenrechner oder einem Software-Tool zur Lösung von Gleichungen finden wir, dass die
Nullstelle bei x ≈ 2.519 ist.
Um Teil (b) zu lösen, betrachten wir die Funktion ga(x) = f(x+a). Wenn wir den Parameter a erhöhen,
verschieben wir den Graph der Funktion f(x) horizontal um die Entfernung a.
Wenn wir positive Werte für a einsetzen, verschiebt sich der Graph nach links. Wenn wir negative Werte
für a einsetzen, verschiebt sich der Graph nach rechts.
Da wir den Graph von f(x) in Bezug auf die Nullstelle x = -1 verschieben wollen, setzen wir a = -1 ein:
ga(x) = f(x+(-1))
= f(x-1)
Durch diese Verschiebung des Graphen von f(x) um 1 Einheit nach rechts erhalten wir den Graphen von
ga(x).
Um einen Wert für a zu finden, sodass die Funktion ga die Nullstelle x = -1 besitzt, setzen wir x = -1 in die
Funktion ga(x) ein und lösen nach a auf:
ga(-1) = f(-1+a) = 0
Wir setzen f(-1+a) gleich null:
1/2*(-1+a)^3 - (-1+a) - 2 = 0
Jetzt können wir diese Gleichung lösen, um den Wert von a zu finden.
1/2*(-1+a)^3 + (1-a) - 2 = 0
Konvertieren wir diese Gleichung in eine quadratische Gleichung:
(-1+a)^3 + 2*(1-a) - 4 = 0
Nun können wir die Gleichung numerisch lösen und es ergibt sich a ≈ -1.851.
Wenn wir a = -1.851 in die Funktion ga(x) = f(x+a) einsetzen, erhalten wir ga(x) = f(x-1.851), wobei der
Graph von ga(x) die Nullstelle x = -1 besitzt.
Aufgabe 5:
1. Untersuchen sie auf Symmetrie: f(x) = 1, 25x^4 − 3x^3 + 1, 1x.
Losung:
Um die Symmetrie einer Funktion zu überprüfen, betrachten wir, ob die
Funktion achsensymmetrisch oder punktsymmetrisch ist.
Eine Funktion f(x) ist achsensymmetrisch, wenn f(x) = f(-x) für alle x im
Definitionsbereich gilt. Das bedeutet, dass der Funktionswert bei x und
-x gleich ist.
Eine Funktion f(x) ist punktsymmetrisch, wenn f(x) = -f(-x) für alle x im
Definitionsbereich gilt. Das bedeutet, dass der Funktionswert bei x das
negative des Funktionswerts bei -x ist.
In diesem Fall betrachten wir die Funktion f(x) = 1,25x^4 - 3x^3 + 1,1x.
Wenn wir f(-x) berechnen, erhalten wir:
f(-x) = 1,25(-x)^4 - 3(-x)^3 + 1,1(-x)
= 1,25x^4 + 3x^3 - 1,1x
Da f(x) nicht gleich f(-x) und auch nicht gleich -f(-x) ist, ist die Funktion
f(x) weder achsensymmetrisch noch punktsymmetrisch. Das bedeutet,
dass die Funktion keine spezielle Symmetrie aufweist.
Stimmt✅